Advertisements
Advertisements
प्रश्न
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
उत्तर
Given that
Construct a ΔABC of given data, AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° and then a triangle similar to it whose sides are (4.5 = 4/5)th of the corresponding sides of ΔABC.
We follow the following steps to construct the given
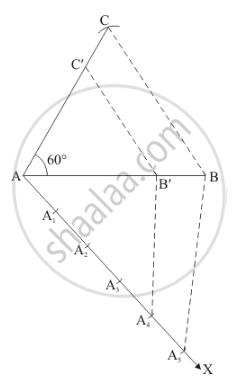
Step of construction
Step: I- First of all we draw a line segment AB = 4.6 cm.
Step: II- With A as centre draw an angle ∠A = 60°.
Step: III- With B as centre and radius = BC = 5.1 cm, draw an arc, intersecting the arc drawn in step II at C.
Step: IV- Joins BC to obtain ΔABC.
Step: V- Below AB, makes an acute angle ∠BAX = 60°.
Step: VI- Along AX, mark off five points A1, A2, A3, A4 and A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5
Step: VII- Join A5B.
Step: VIII- Since we have to construct a triangle each of whose sides is (4/5)th of the corresponding sides of ΔABC.
So, we take four parts out of five equal parts on AX from point A4 draw A4B' || A5B, and meeting AB at B’.
Step: IX- From B’ draw B'C' || BC and meeting AC at C’
Thus, ΔAB'C' is the required triangle, each of whose sides is (4/5)th of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
By geometrical construction, it is possible to divide a line segment in the ratio ______.
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
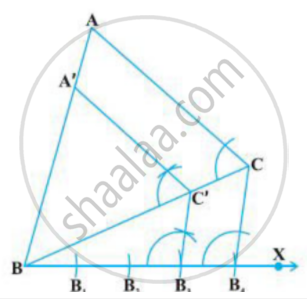
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
Draw a line segment of length 7 cm and divide it in the ratio 5 : 3.
