Question

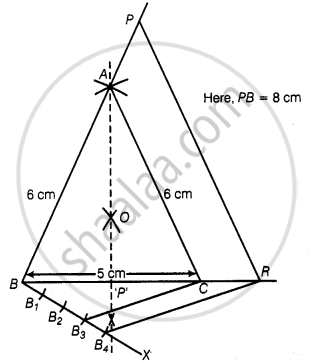
Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PQR similar to ∆ABC in which PQ = 8 cm. Also justify the construction.

Answer 1

Let ΔPQR and ΔABC are similar triangles, then its scale factor between the corresponding sides is `"PQ"/"AB" = 8/6 = 4/3`

Steps of construction:

1. Draw a line segment BC = 5 cm.
2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P’.
3. Taking B and C as centres draw two arcs of equal radius 6 cm intersecting each other at A.
4. Join BA and CA. So, ΔABC is the required isosceles triangle.
5. From B, draw any ray BX making an acute ∠CBX.
6. Locate four points B₁, B₂, B₃ and B₄ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
7. Join B₃C and from B₄ draw a line B₄R || B₃C intersecting the extended line segment BC at R.
8. From point R, draw RP || CA meeting BA produced at P.
   Then, ΔPBR is the required triangle.

Justification:

∵ B₄R || B₃C    ...(By construction)

∴ `"BC"/"CR" = 3/1`

Now, `"BR"/"BC" = ("BC" + "CR")/"BC"`

= `1 + "CR"/"BC"`

= `1 + 1/3`

= `4/3`

Also, RP || CA

∴ ΔABC ∼ ΔPBR

And `"PB"/"AB" = "RP"/"CA" = "BR"/"BC" = 4/3`

Hence, the new triangle is similar to the given whose sides are `4/3` times of the corresponding sides of the isosceles ΔABC.