Advertisements
Advertisements
प्रश्न
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
उत्तर
Construct a right triangle of sides \[AB = 4 cm, AC = 3 cm \text { and } \angle A = 90^\circ \] and then a triangle similar to it whose sides are \[\left( \frac{3}{5} \right)^{th}\]
of the corresponding sides of ΔABC.
We follow the following steps to construct the given
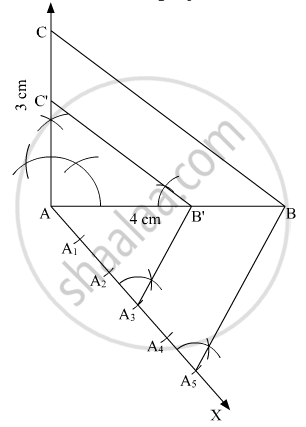
Step of construction
Step: I- First of all we draw a line segment AB = 4 cm.
Step: II- With A as centre and draw an angle ∠A = 90°.
Step: III- With A as centre and radius AC = 3 cm.
Step: IV-Join BC to obtain right ΔABC.
Step: V- Below AB, makes an acute angle \[\angle BAX\].
Step: VI- Along AX, mark off five points \[A_1 , A_2 , A_3 , A_4 \text { and } A_5\] such that `A A_1 = A_1A_2 = A_2 A_3 = A_3 A_4` \[= A_4 A_5\]
Step: VII- Join \[A_5 B\].
Step: VIII -Since we have to construct a triangle each of whose sides is \[\left( \frac{3}{5} \right)^{th}\] of the corresponding sides of right ΔABC.
So, we draw a line `A_3B' `on AX from point `A_3`which is \[A_3 B \lVert A_5 B\] and meeting AB at B’.
Step: IX- From B’ point draw B'C' || BC, and meeting AC at C’
Thus, ΔAB'C'is the required triangle, each of whose sides is \[\left( \frac{3}{5} \right)^{th}\] of the corresponding sides of ΔAB.
APPEARS IN
संबंधित प्रश्न
Construct an isosceles triangle with base 8 cm and altitude 4 cm. Construct another triangle whose sides are `2/3` times the corresponding sides of the isosceles triangle.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Δ AMT ∼ ΔAHE. In Δ AMT, MA = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `(MA)/(HA) = 7/5`. construct Δ AHE.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Find the ratio in which the segment joining the points (1, –3) and (4, 5) is divided by the x-axis? Also, find the coordinates of this point on the x-axis.
Draw the line segment AB = 5cm. From the point A draw a line segment AD = 6cm making an angle of 60° with AB. Draw a perpendicular bisector of AD. Select the correct figure.
The basic principle used in dividing a line segment is ______.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Construct a triangle similar to ∆ABC with scale factor `5/7`. Justify the construction.
