Question

Construct an isosceles triangle with base 8 cm and altitude 4 cm. Construct another triangle whose sides are `2/3` times the corresponding sides of the isosceles triangle.

Answer 1

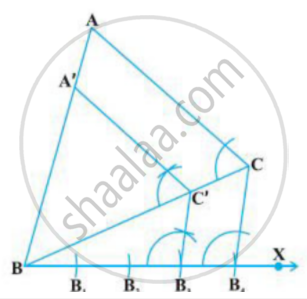
Steps of Construction

Step 1. Draw a line segment BC = 8 cm.

Step 2. Draw the perpendicular bisector XY of BC, cutting BC at D.

Step 3. With D as centre and radius 4 cm, draw an arc cutting XY at A.

Step 4. Join AB and AC. Here, ∆ABC is an isosceles whose base is 8 cm and altitude is 4 cm.

Step 5. Below BC, draw an acute angle ∠CBX.

Step 6. Along BX, mark three points B₁, B₂ and B₃ such that BB₁ = B₁B₂ = B₂B₃.

Step 7. Join CB₃.

Step 8. From B₂, draw B₂C' || CB₃ meeting BC at C'.

Step 9. From C', draw A'C' || AC meeting AB in A'.

Here, ∆A'BC' is the required triangle similar to ∆ABC such that each side of ∆A'BC' is `2/3` times the corresponding side of ∆ABC.