Advertisements
Advertisements
प्रश्न
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
उत्तर
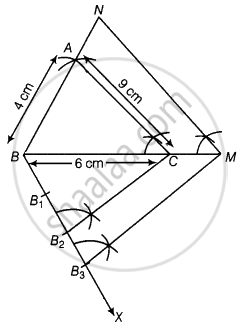
Steps of construction:
- Draw a line segment BC = 6 cm.
- Taking B and C as centres, draw two arcs of radii 4 cm and 9 cm intersecting each other at A.
- Join BA and CA, ΔABC is the required triangle.
- From B, draw any ray BX downwards making an acute angle.
- Mark three points B1, B2, B3 on BX, such that BB1 = B1B2 = B2B3.
- Join B2C and from B3 draw B3M || B2C intersecting the extended line segment BC at M.
- From point M, draw MN || CA intersecting the extended line segment BA to N.
Then, ΔNBM is the required triangle whose sides are equals to `3/2` of the corresponding sides of the ΔABC.
Justification:
Here, B3M || B2C
∴ `"BC"/"CM" = 2/1`
Now, `"BM"/"BC" = ("BC" + "CM")/"BC"`
= `1 + "CM"/"BC"`
= `1 + 1/2`
= `3/2`
Also, MN || CA
∴ ΔABC ∼ ΔNBM
Therefore, `"NB"/"AB" = "NM"/"AC" = "BM"/"BC" = 3/2`
The two triangles are not congruent because, if two triangles are congruent, then they have same shape and same size. Here, all the three angles are same but three sides are not same i.e., one side is different.
APPEARS IN
संबंधित प्रश्न
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Points P and Q trisect the line segment joining the points A(−2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
To divide a line segment AB in the ratio p : q (p, q are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is ______.
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, ... and B1, B2, B3, ... are located at equal distances on ray AX and BY, respectively. Then the points joined are ______.
A triangle ABC is such that BC = 6cm, AB = 4cm and AC = 5cm. For the triangle similar to this triangle with its sides equal to `3/4`th of the corresponding sides of ΔABC, correct figure is?
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The basic principle used in dividing a line segment is ______.
