Advertisements
Advertisements
Question
The line segment AB is divided into five congruent parts at P, Q, R and S such that A–P–Q–R–S–B. If point Q(12, 14) and S(4, 18) are given find the coordinates of A, P, R, B.
Advertisements
Solution
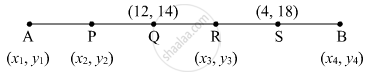
Points P, Q, R and S divide seg AB in five congruent parts.
Let A x1, y1), B(x2, y2), P(x3, y3) and R(x4, y4) be the given points.
Point R is the midpoint of segment QS.
By midpoint formula,
x co-ordinate of R = `(12 + 4)/2 = 16/2` = 8
y co-ordinate of R = `(14 + 18)/2 = 32/2` = 16
RELATED QUESTIONS
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
Points P and Q trisect the line segment joining the points A(−2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
Construct an equilateral ∆ABC with side 5 cm. ∆ABC ~ ∆LMN, ratio the corresponding sides of triangle is 6 : 7, then construct ΔLMN and ΔABC
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To divide a line segment AB in the ratio p : q (p, q are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is ______.
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is ______.
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
To construct a triangle similar to a given ΔABC with its sides `3/7` of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3, ... on BX at equal distances and next step is to join ______.
A triangle ABC is such that BC = 6cm, AB = 4cm and AC = 5cm. For the triangle similar to this triangle with its sides equal to `3/4`th of the corresponding sides of ΔABC, correct figure is?
The ratio of corresponding sides for the pair of triangles whose construction is given as follows: Triangle ABC of dimensions AB = 4cm, BC = 5 cm and ∠B= 60°.A ray BX is drawn from B making an acute angle with AB.5 points B1, B2, B3, B4 and B5 are located on the ray such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
B4 is joined to A and a line parallel to B4A is drawn through B5 to intersect the extended line AB at A’.
Another line is drawn through A’ parallel to AC, intersecting the extended line BC at C’. Find the ratio of the corresponding sides of ΔABC and ΔA′BC′.
If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
What is the ratio `(AC)/(BC)` for the following construction: A line segment AB is drawn. A single ray is extended from A and 12 arcs of equal lengths are cut, cutting the ray at A1, A2… A12.A line is drawn from A12 to B and a line parallel to A12B is drawn, passing through the point A6 and cutting AB at C.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor `2/3`. Is the new triangle also a right triangle?
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
Draw a line segment of length 7 cm and divide it in the ratio 5 : 3.
