Question

Find the coordinates of the centre of the circle passing through the points P(6, –6), Q(3, –7) and R (3, 3).

Answer 1

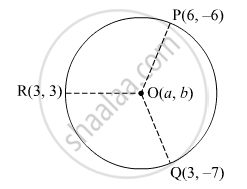
Let O(a, b) be the centre of the circle.

Let the points (6,- 6), (3, -7), and (3, 3) represent the points P, Q, and R on the circumference of the circle.

Distance from centre O to P, Q, R are found below using the Distance formula.

Distance Formula = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`

From the figure ,

OP = OQ      ...(radii of the same circle)

`∴ sqrt((a - 6)^2 + (b - (- 6))^2) = sqrt((a - 3)^2 + (b - (- 7))^2)`

`∴ sqrt((a - 6)^2 + (b + 6)^2) = sqrt((a - 3)^2 + (b + 7)^2)`

Squaring on both sides,

(a - 6)² + (b + 6)² = (a - 3)² + (b + 7)²

∴ a² - 12a + 36 + b² + 12b + 36 = a² - 6a + 9 + b² + 14b + 49

∴ 3a + b = 7     ...(1)  

OP = OR        ...(radii of the same circle)

`∴ sqrt((a - 6)^2 + (b - (- 6))^2) = sqrt((a - 3)^2 + (b - 3)^2)`

`∴ sqrt((a - 6)^2 + (b + 6)^2) = sqrt((a - 3)^2 + (b - 3)^2)`

Squaring on both sides,

(a - 6)² + (b + 6)² = (a - 3)² + (b - 3)²

∴ a² - 12a + 36 + b² + 12b + 36 = a² - 6a + 9 + b² - 6b + 9

54 = 6a + 18

∴ a - 3b = 9     ...(2)

Multiplying (2) with 3, we get,

∴ 3a - 9b = 27      ...(3)

Subtracting equation (3) from (1),

\[\begin{array}{l}  
\phantom{\texttt{0}}\texttt{3a + b = 7}\\ \phantom{\texttt{}}\texttt{-3a - 9b = 27}\\ \hline\phantom{\texttt{}}\texttt{(-) (+) (-)}\\ \hline \end{array}\]
∴ 10b = - 20
∴ b = - 2

Substituting b = - 2 in equation (1),

3a + b = 7  
3a - 2 = 7
3a = 7 + 2
3a = 9
a = 3

Coordinates of centre of the circle are (3, -2) .