Advertisements
Advertisements
Question
Show that `square` ABCD formed by the vertices A(-4,-7), B(-1,2), C(8,5) and D(5,-4) is a rhombus.
Solution
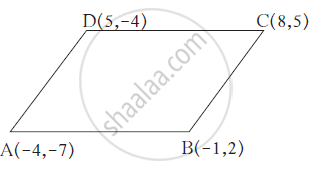
`AD = sqrt((X_2 -X_1)^2 +(Y_2 -Y_1)^2)`
`=sqrt(((5+4)^2 +(-4+7)^2`
`=sqrt(81+9)`
=`sqrt90`
=`3sqrt10 ................. (1)`
BC =`sqrt((8+1)^2 + (5-2)^2)`
`=sqrt(81+9)`
=`sqrt90`
`=3sqrt10 ............(2)`
`AB = sqrt(-1+4)^2 +(2+7)^2`
`=sqrt9+81`
`=sqrt90`
`=3sqrt10` ...............(3)
`CD = sqrt((8-5)^2 +(5+4)^2)`
`=sqrt(9+81)`
`=sqrt90`
`=3sqrt10 ` ...............(4)
From (1), (2), (3) and (4); AB = BC = CD = DA
∴ `square` ABCD is a rhombus.
APPEARS IN
RELATED QUESTIONS
How will you describe the position of a table lamp on your study table to another person?
Find the distance between the following pair of points:
(a, 0) and (0, b)
Show that the points A(5, 6), B(1, 5), C(2, 1) and D(6,2) are the vertices of a square.
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P when AP/BP = 3/4.
Determine the ratio in which the point P (m, 6) divides the join of A(-4, 3) and B(2, 8). Also, find the value of m.
Point A lies on the line segment PQ joining P(6, -6) and Q(-4, -1) in such a way that `(PA)/( PQ)=2/5` . If that point A also lies on the line 3x + k( y + 1 ) = 0, find the value of k.
If the point `P (1/2,y)` lies on the line segment joining the points A(3, -5) and B(-7, 9) then find the ratio in which P divides AB. Also, find the value of y.
Prove that the diagonals of a rectangle ABCD with vertices A(2,-1), B(5,-1) C(5,6) and D(2,6) are equal and bisect each other
If the point C(k,4) divides the join of A(2,6) and B(5,1) in the ratio 2:3 then find the value of k.
Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4) ?
Find the coordinates of the circumcentre of a triangle whose vertices are (–3, 1), (0, –2) and (1, 3).
If `P(a/2,4)`is the mid-point of the line-segment joining the points A (−6, 5) and B(−2, 3), then the value of a is
The abscissa and ordinate of the origin are
Points (−4, 0) and (7, 0) lie
If A(3, y) is equidistant from points P(8, −3) and Q(7, 6), find the value of y and find the distance AQ.
Find the coordinates of the point which is equidistant from the three vertices A (\[2x, 0) O (0, 0) \text{ and } B(0, 2y) of ∆\] AOB .
The ratio in which the x-axis divides the segment joining (3, 6) and (12, −3) is
The coordinates of a point whose ordinate is `-1/2` and abscissa is 1 are `-1/2, 1`.
