Advertisements
Advertisements
Question
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
Notes
We have two points P (3, 3) and Q (6,−6). There are two points A and B which trisect the line segment joining P and Q.
Let the co-ordinate of A be `A (x_1, y_1)`
Now according to the section formula if any point P divides a line segment joining `A(x_1, y_1)` and `B(x_2, y_2)` in the ratio m: n internally than,
`P(x,y) = ((nx_1 + mx_2)/(m + n), (ny_1 + my_2)/(m + n))`
The point A is the point of trisection of the line segment PQ. So, A divides PQ in the ratio 1: 2
Now we will use section formula to find the coordinates of unknown point A as,
`A(x,y ) = ((2(3) + 1(6))/(1 + 2)"," (2(3) + 1(-6))/(1 + 2))`
Therefore, co-ordinates of point A is(4, 0)
It is given that point A lies on the line whose equation is
2x + y + k = 0
So point A will satisfy this equation.
2(4) + 0 + k = 0
So,
k = -8
APPEARS IN
RELATED QUESTIONS
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
- how many cross - streets can be referred to as (4, 3).
- how many cross - streets can be referred to as (3, 4).
Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
Prove that the points (0, 0), (5, 5) and (-5, 5) are the vertices of a right isosceles triangle.
In the seating arrangement of desks in a classroom three students Rohini, Sandhya and Bina are seated at A(3, 1), B(6, 4), and C(8, 6). Do you think they are seated in a line?
The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the coordinates of the fourth vertex.
Show that the following points are the vertices of a rectangle.
A (2, -2), B(14,10), C(11,13) and D(-1,1)
If the point P(k-1, 2) is equidistant from the points A(3,k) and B(k,5), find the value of k.
The points \[A \left( x_1 , y_1 \right) , B\left( x_2 , y_2 \right) , C\left( x_3 , y_3 \right)\] are the vertices of ΔABC .
(i) The median from A meets BC at D . Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such thatBQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centropid of the triangle ABC ?
If R (x, y) is a point on the line segment joining the points P (a, b) and Q (b, a), then prove that x + y = a + b.
If the centroid of the triangle formed by points P (a, b), Q(b, c) and R (c, a) is at the origin, what is the value of a + b + c?
Find the value of a so that the point (3, a) lies on the line represented by 2x − 3y + 5 = 0
If the distance between the points (3, 0) and (0, y) is 5 units and y is positive. then what is the value of y?
Find the coordinates of the point which is equidistant from the three vertices A (\[2x, 0) O (0, 0) \text{ and } B(0, 2y) of ∆\] AOB .
If the distance between the points (4, p) and (1, 0) is 5, then p =
A line segment is of length 10 units. If the coordinates of its one end are (2, −3) and the abscissa of the other end is 10, then its ordinate is
If points (t, 2t), (−2, 6) and (3, 1) are collinear, then t =
The length of a line segment joining A (2, −3) and B is 10 units. If the abscissa of B is 10 units, then its ordinates can be
The coordinates of two points are P(4, 5) and Q(–1, 6). Find the difference between their abscissas.
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
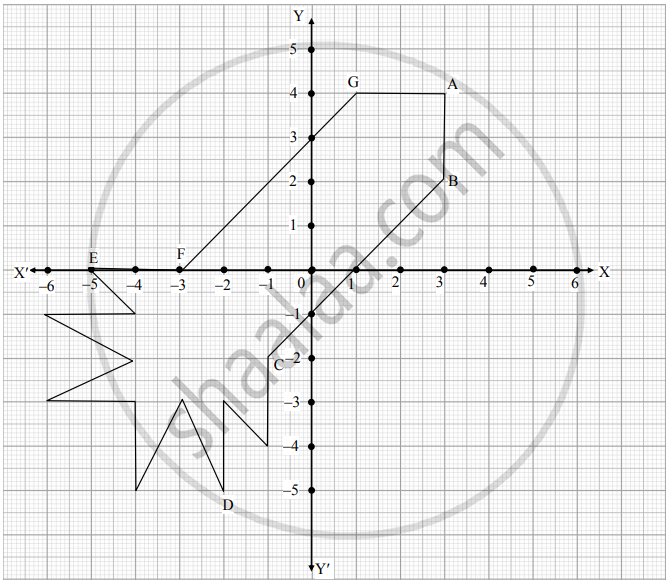
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
