Question

(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.

All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.

There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2^nd street running in the North - South direction and 5^th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:

1. how many cross - streets can be referred to as (4, 3).
2. how many cross - streets can be referred to as (3, 4).

Answer 1

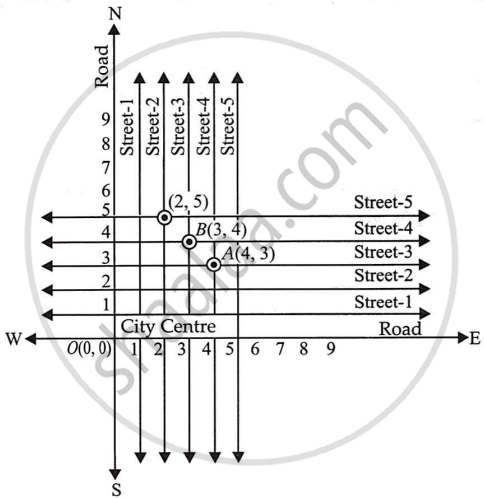
1. Point A(4, 3) shows a unique cross street.
2. A unique cross street is shown at point B(3, 4).

The two cross streets are uniquely found because of the two reference lines we have used to locate them.