Advertisements
Advertisements
Question
How will you describe the position of a table lamp on your study table to another person?
Advertisements
Solution 1
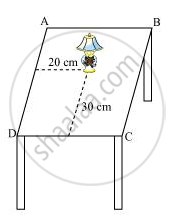
Consider that the lamp is placed on the table. Choose two adjacent edges, DC and AD. Then, draw perpendiculars on the edges of DC and AD from the position of the lamp and measure the lengths of these perpendiculars. Let the length of these perpendiculars be 30 cm and 20 cm, respectively. Now, the position of the lamp from the left edge (AD) is 20 cm and from the lower edge (DC) is 30 cm. This can also be written as (20, 30), where 20 represents the perpendicular distance of the lamp from edge AD and 30 represents the perpendicular distance of the lamp from edge DC.
Solution 2
To describe the position of a mobile phone kept on the study table, we take two lines, a perpendicular and a horizontal line.
Considering the table as a plane(x and y axis) and taking perpendicular line as Y axis and horizontal as X axis respectively. Take one corner of table as origin where both X and Y axes intersect each other. Now, the length of table is Y axis and breadth is X axis. From The origin, join the line to the mobile phone and mark a point. The distances of the point from both the X and Y axes should be calculated and then written in terms of coordinates.
Let the distance of the point from X- axis and Y- axis is x and y respectively, so the mobile phone will be in (x, y) coordinate.
APPEARS IN
RELATED QUESTIONS
Find the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
Show that the points A (1, 0), B (5, 3), C (2, 7) and D (−2, 4) are the vertices of a parallelogram.
In what ratio does the point (−4, 6) divide the line segment joining the points A(−6, 10) and B(3,−8)?
Point P(x, 4) lies on the line segment joining the points A(−5, 8) and B(4, −10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
Show that A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a
rhombus ABCD.
A point whose abscissa is −3 and ordinate 2 lies in
Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
Two vertices of a triangle have coordinates (−8, 7) and (9, 4) . If the centroid of the triangle is at the origin, what are the coordinates of the third vertex?
The points whose abscissa and ordinate have different signs will lie in ______.
