Advertisements
Advertisements
प्रश्न
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
- how many cross - streets can be referred to as (4, 3).
- how many cross - streets can be referred to as (3, 4).
उत्तर
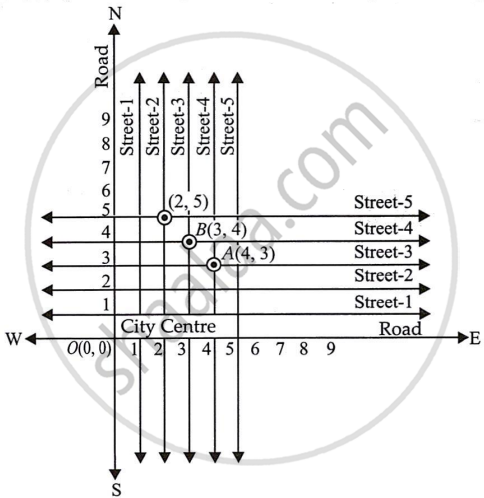
- Point A(4, 3) shows a unique cross street.
- A unique cross street is shown at point B(3, 4).
The two cross streets are uniquely found because of the two reference lines we have used to locate them.
APPEARS IN
संबंधित प्रश्न
On which axis do the following points lie?
S(0,5)
If G be the centroid of a triangle ABC, prove that:
AB2 + BC2 + CA2 = 3 (GA2 + GB2 + GC2)
Points P, Q, R and S divides the line segment joining A(1, 2) and B(6, 7) in 5 equal parts. Find the coordinates of the points P, Q and R.
If x is a positive integer such that the distance between points P (x, 2) and Q (3, −6) is 10 units, then x =
The perimeter of the triangle formed by the points (0, 0), (0, 1) and (0, 1) is
The coordinates of the fourth vertex of the rectangle formed by the points (0, 0), (2, 0), (0, 3) are
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
If segment AB is parallel Y-axis and coordinates of A are (1, 3), then the coordinates of B are ______
If the coordinate of point A on the number line is –1 and that of point B is 6, then find d(A, B).
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1:2.
Reason (R): as formula for the internal division is `((mx_2 + nx_1)/(m + n) , (my_2 + ny_1)/(m + n))`
