Advertisements
Advertisements
Question
Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4) ?
Solution
Let A(3, –2) and B(–3, –4) be the two given points.
Suppose P(x1, y1) and Q(x2, y2) are the points of trisection of the line segment joining the given points i.e. AP = PQ = QB.
Now,
PB = PQ + QB = AP + AP = 2AP
∴ AP : PB = AP : 2AP = 1 : 2
So, point P divides AB internally in the ratio 1 : 2.
Similarly,
AQ : QB = 2 : 1
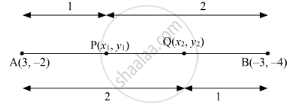
P divides AB internally in the ratio 1 : 2.
\[\therefore \left( \frac{1 \times \left( - 3 \right) + 2 \times 3}{1 + 2}, \frac{1 \times \left( - 4 \right) + 2 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow \left( \frac{- 3 + 6}{3}, \frac{- 4 - 4}{3} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow \left( 1, - \frac{8}{3} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow x_1 = 1, y_1 = - \frac{8}{3}\]
Q divides AB internally in the ratio 2 : 1.
\[\therefore \left( \frac{2 \times \left( - 3 \right) + 1 \times 3}{1 + 2}, \frac{2 \times \left( - 4 \right) + 1 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow \left( \frac{- 6 + 3}{3}, \frac{- 8 - 2}{3} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow \left( - 1, - \frac{10}{3} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow x_2 = - 1, y_2 = - \frac{10}{3}\]
Thus, the coordinates of the points of trisection of the line segment joining the given points are
APPEARS IN
RELATED QUESTIONS
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively.
Find the points of trisection of the line segment joining the points:
(2, -2) and (-7, 4).
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
Show that the points A (1, 0), B (5, 3), C (2, 7) and D (−2, 4) are the vertices of a parallelogram.
In what ratio does the point (−4, 6) divide the line segment joining the points A(−6, 10) and B(3,−8)?
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
If the point `P (1/2,y)` lies on the line segment joining the points A(3, -5) and B(-7, 9) then find the ratio in which P divides AB. Also, find the value of y.
Prove that the diagonals of a rectangle ABCD with vertices A(2,-1), B(5,-1) C(5,6) and D(2,6) are equal and bisect each other
If the point C(k,4) divides the join of A(2,6) and B(5,1) in the ratio 2:3 then find the value of k.
Find the coordinates of circumcentre and radius of circumcircle of ∆ABC if A(7, 1), B(3, 5) and C(2, 0) are given.
If the point P(x, 3) is equidistant from the point A(7, −1) and B(6, 8), then find the value of x and find the distance AP.
If A(3, y) is equidistant from points P(8, −3) and Q(7, 6), find the value of y and find the distance AQ.
Find the value of k if points A(k, 3), B(6, −2) and C(−3, 4) are collinear.
Write the ratio in which the line segment doining the points A (3, −6), and B (5, 3) is divided by X-axis.
The coordinates of the point on X-axis which are equidistant from the points (−3, 4) and (2, 5) are
If the sum of X-coordinates of the vertices of a triangle is 12 and the sum of Y-coordinates is 9, then the coordinates of centroid are ______
Abscissa of all the points on the x-axis is ______.
The points whose abscissa and ordinate have different signs will lie in ______.
If the points P(1, 2), Q(0, 0) and R(x, y) are collinear, then find the relation between x and y.
Given points are P(1, 2), Q(0, 0) and R(x, y).
The given points are collinear, so the area of the triangle formed by them is `square`.
∴ `1/2 |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)| = square`
`1/2 |1(square) + 0(square) + x(square)| = square`
`square + square + square` = 0
`square + square` = 0
`square = square`
Hence, the relation between x and y is `square`.
