Advertisements
Advertisements
प्रश्न
Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4) ?
उत्तर
Let A(3, –2) and B(–3, –4) be the two given points.
Suppose P(x1, y1) and Q(x2, y2) are the points of trisection of the line segment joining the given points i.e. AP = PQ = QB.
Now,
PB = PQ + QB = AP + AP = 2AP
∴ AP : PB = AP : 2AP = 1 : 2
So, point P divides AB internally in the ratio 1 : 2.
Similarly,
AQ : QB = 2 : 1
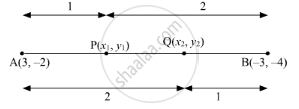
P divides AB internally in the ratio 1 : 2.
\[\therefore \left( \frac{1 \times \left( - 3 \right) + 2 \times 3}{1 + 2}, \frac{1 \times \left( - 4 \right) + 2 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow \left( \frac{- 3 + 6}{3}, \frac{- 4 - 4}{3} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow \left( 1, - \frac{8}{3} \right) = \left( x_1 , y_1 \right)\]
\[ \Rightarrow x_1 = 1, y_1 = - \frac{8}{3}\]
Q divides AB internally in the ratio 2 : 1.
\[\therefore \left( \frac{2 \times \left( - 3 \right) + 1 \times 3}{1 + 2}, \frac{2 \times \left( - 4 \right) + 1 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow \left( \frac{- 6 + 3}{3}, \frac{- 8 - 2}{3} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow \left( - 1, - \frac{10}{3} \right) = \left( x_2 , y_2 \right)\]
\[ \Rightarrow x_2 = - 1, y_2 = - \frac{10}{3}\]
Thus, the coordinates of the points of trisection of the line segment joining the given points are
APPEARS IN
संबंधित प्रश्न
Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
Which point on the y-axis is equidistant from (2, 3) and (−4, 1)?
Find the value of k, if the point P (0, 2) is equidistant from (3, k) and (k, 5).
Find the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3,5).
If the points p (x , y) is point equidistant from the points A (5,1)and B ( -1,5) , Prove that 3x=2y
Find the coordinates of the midpoints of the line segment joining
A(3,0) and B(-5, 4)
`"Find the ratio in which the poin "p (3/4 , 5/12) " divides the line segment joining the points "A (1/2,3/2) and B (2,-5).`
In what ratio does the line x - y - 2 = 0 divide the line segment joining the points A (3, 1) and B (8, 9)?
Find the area of quadrilateral ABCD whose vertices are A(-3, -1), B(-2,-4) C(4,-1) and D(3,4)
Find the centroid of ΔABC whose vertices are A(2,2) , B (-4,-4) and C (5,-8).
If the points A (2,3), B (4,k ) and C (6,-3) are collinear, find the value of k.
Find the value of k, if the points A(7, −2), B (5, 1) and C (3, 2k) are collinear.
If the point P (m, 3) lies on the line segment joining the points \[A\left( - \frac{2}{5}, 6 \right)\] and B (2, 8), find the value of m.
If the mid-point of the segment joining A (x, y + 1) and B (x + 1, y + 2) is C \[\left( \frac{3}{2}, \frac{5}{2} \right)\] , find x, y.
If points Q and reflections of point P (−3, 4) in X and Y axes respectively, what is QR?
Find the values of x for which the distance between the point P(2, −3), and Q (x, 5) is 10.
Find the distance between the points \[\left( - \frac{8}{5}, 2 \right)\] and \[\left( \frac{2}{5}, 2 \right)\] .
If x is a positive integer such that the distance between points P (x, 2) and Q (3, −6) is 10 units, then x =
Assertion (A): Mid-point of a line segment divides the line segment in the ratio 1 : 1
Reason (R): The ratio in which the point (−3, k) divides the line segment joining the points (− 5, 4) and (− 2, 3) is 1 : 2.
