Question

Find the coordinates of the points of trisection of the line segment joining the points (3, –2) and (–3, –4) ?

Answer 1

Let A(3, –2) and B(–3, –4) be the two given points.

Suppose P(x₁, y₁) and Q(x₂, y₂) are the points of trisection of the line segment joining the given points i.e. AP = PQ = QB.

Now,

PB = PQ + QB = AP + AP = 2AP

∴ AP : PB = AP : 2AP = 1 : 2

So, point P divides AB internally in the ratio 1 : 2.

Similarly,

AQ : QB = 2 : 1

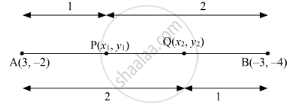
P divides AB internally in the ratio 1 : 2.

\[\therefore \left( \frac{1 \times \left( - 3 \right) + 2 \times 3}{1 + 2}, \frac{1 \times \left( - 4 \right) + 2 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_1 , y_1 \right)\]

\[ \Rightarrow \left( \frac{- 3 + 6}{3}, \frac{- 4 - 4}{3} \right) = \left( x_1 , y_1 \right)\]

\[ \Rightarrow \left( 1, - \frac{8}{3} \right) = \left( x_1 , y_1 \right)\]

\[ \Rightarrow x_1 = 1, y_1 = - \frac{8}{3}\]

Q divides AB internally in the ratio 2 : 1.

\[\therefore \left( \frac{2 \times \left( - 3 \right) + 1 \times 3}{1 + 2}, \frac{2 \times \left( - 4 \right) + 1 \times \left( - 2 \right)}{1 + 2} \right) = \left( x_2 , y_2 \right)\]

\[ \Rightarrow \left( \frac{- 6 + 3}{3}, \frac{- 8 - 2}{3} \right) = \left( x_2 , y_2 \right)\]

\[ \Rightarrow \left( - 1, - \frac{10}{3} \right) = \left( x_2 , y_2 \right)\]

\[ \Rightarrow x_2 = - 1, y_2 = - \frac{10}{3}\]

Thus, the coordinates of the points of trisection of the line segment joining the given points are 

\[\left( 1, - \frac{8}{3} \right) and \left( - 1, - \frac{10}{3} \right) .\]