Advertisements
Advertisements
प्रश्न
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `3/5` of the corresponding sides of the first triangle.
उत्तर

1. Draw a line AB = 5 cm and draw a ray from A and taking A as centre cut an arc at C of 6 cm and taking B as centre cut an arc of 7 cm at C
2. Draw AX such that ∠BAX is an acute angle.
3. Cut 5 equal arcs AA1, A1A2, A2A3, A3A4, and A4A5.
4. Join A5 to B and draw a line through A3 parallel to A5B which meets AB at B'.
Here, `AB' = 3/5AB`
5. Now draw a line through B' parallel to BC which joins AC at C'.
Here, `B'C' = 3/5BC "and" AC' = 3/5AC`
Thus, AB'C' is the required triangle.
APPEARS IN
संबंधित प्रश्न
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

In ΔABC and ΔDEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE=10cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL: DM.
State, true or false:
Two congruent polygons are necessarily similar.
The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ΔAPQ is 116 of the area of ΔABC.
State the SSS-similarity criterion for similarity of triangles
As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?

ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"EC"`
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
Two similar triangles will always have ________ angles
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

Observe the figure and complete the following activity

In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
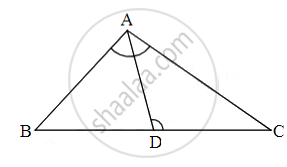
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
