Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
उत्तर
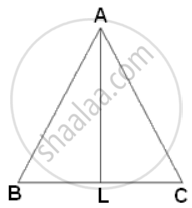
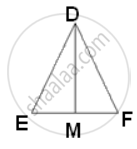
The ratio of the areas of two similar triangles is equal to the ratio of the square of the corresponding altitudes.
∴ `("area"(Δ"ABC"))/("area"(Δ"PQR")) = "AL"^2/"DM"^2`
⇒ `(16)/(9) = "AL"^2/1.8^2`
⇒ AL2 = `(16 xx 3.24)/(9)`
⇒ AL2 = 5.76
⇒ AL = 2.4cm.
APPEARS IN
संबंधित प्रश्न
E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC , if DP ⊥ AB and DQ ⊥ BC then prove that
`(a) DQ^2 Dp.QC (b) DP ^2 DQ.AP 2 `

On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD is measured as AB= 12 cm and BC = 16cm. calculate the diagonal distance of the plot in km and the plot area in km2 .
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

Sides of a triangle are 7, 24 and 25. Determine whether the triangle is a right-angled triangle or not.
In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
