Advertisements
Advertisements
Question
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4, AE = 8, DB = x - 4 and EC = 3x - 19, find x.
Solution
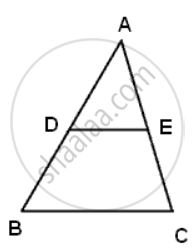
In ΔADE and ΔABC
∠D = ∠B and ∠C = ∠E ...(DE || BC)
⇒ ΔADE ∼ ΔABC
∴ `"AD"/"DB" = "AE"/"EC"`
⇒ `(4)/(x - 4) = (8)/(3x - 19)`
⇒ 4 x (3x - 19) = 8x (x - 4)
⇒ 12x - 76 = 8x - 32
⇒ 4x = 44
⇒ x = 11.
APPEARS IN
RELATED QUESTIONS
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.

O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that ΔPTQ - DRTS
In the given figure, if ΔEAT ~ ΔBUN, find the measure of all angles.
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
