Advertisements
Advertisements
Question
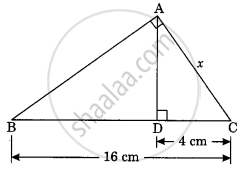
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
Solution
Here, AC and PR represent the bigger and smaller poles, and BC and QR represent their shadows respectively.
Now,
ΔACB ∼ ΔPRQ .....[Vertical poles and their shadows form similar figures]
∴ `"CB"/"RQ" = "AC"/"PR"` ......[Corresponding sides of similar triangles]
∴ `x/6 = 8/4`
∴ x = `(8 xx 6)/4`
∴ x = 12 m
∴ The shadow of the bigger pole will be 12 metres long at that time.
APPEARS IN
RELATED QUESTIONS
In the given figure ABC is a triangle with ∠EDB = ∠ACB. Prove that Δ ABC ~ Δ EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm. And area of Δ BED = 9 cm2. Calculate the
(1) length of AB
(2) area of Δ ABC
The two similar triangles are equal in area. Prove that the triangles are congruent.
ΔABC~ΔDEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
State the SSS-similarity criterion for similarity of triangles
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?
On a map drawn to a scale of 1 : 25000, a triangular plot of a land is marked as ABC with AB= 6cm, BC = 8cm and ∠ ABC = 90° . Calculate the actual length of AB in km and the actual area of the plot in km2 .
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.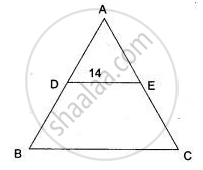
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.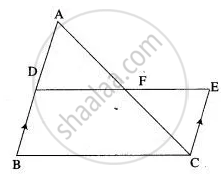
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
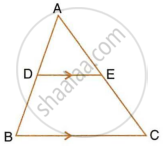
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3,Find x.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 5.6cm, AD = 1.4cm, AC = 7.2cm, and AE = 1.8cm
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
If in triangles ABC and EDF, `"AB"/"DE" = "BC"/"FD"` then they will be similar, when
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
Observe the figure and complete the following activity
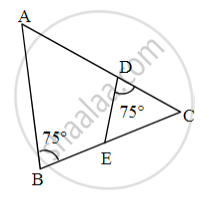
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
In the given figure the value of x is