Advertisements
Advertisements
Question
State the AA-similarity criterion
Solution
If two angles are correspondingly equal to the two angles of another triangle, then the two triangles are similar.
APPEARS IN
RELATED QUESTIONS
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`
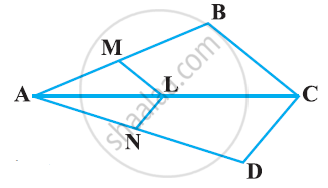
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
State, true or false:
All isosceles triangles are similar.
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.

In Δ ABC , DE is parallel to BC and `"AD"/"DB" = 2/7` IF AC = 5 .6 , find AE.
In Δ ABC , MN || BC .
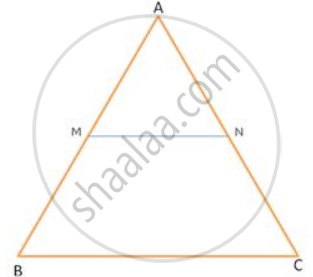
If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
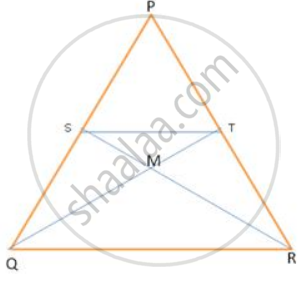
Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
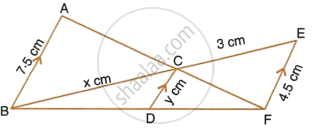
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.
Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.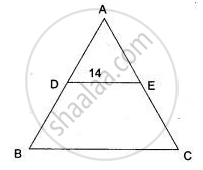
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`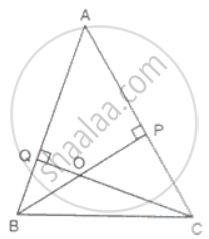
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.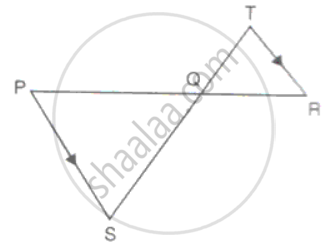
In the figure, DE || AC and DC || AP. Prove that `"BE"/"EC" = "BC"/"CP"`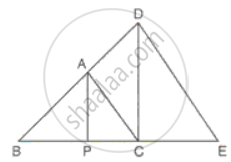
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that TP:TQ = TR:TS
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
Check whether the triangles are similar and find the value of x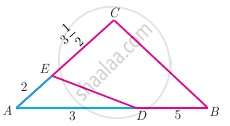
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
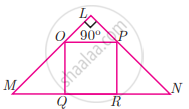
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN
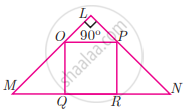
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
