Advertisements
Advertisements
Question
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
Solution
ABCD is a square. ∆BCE is described on side BC is similar to ∆ACF described on diagonal AC.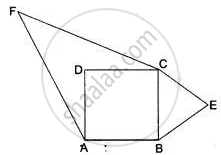
Since ABCD is a square. Therefore,
AB = BC = CD = DA
and AC = `sqrt(2)"BC"` ...[∵ Diagonal = `sqrt(2)` (side)]
Now, ∆BCE ~ ∆ACF
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BC"^2/"AC"^2`
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BF"^2/(sqrt(2)"BC")^2 = (1)/(2)`
⇒ Area (∆BCE) = `(1)/(2) "area (∆ACF)"`.
Hence proved.
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles-right triangles are similar.
On a map, drawn to a scale of 1 : 250000, a triangular plot PQR of land has the following measurements :
PQ = 3cm, QR = 4 cm and angles PQR = 90°
(i) the actual lengths of QR and PR in kilometer.
(ii) the actual area of the plot in sq . km.
A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.

The dimensions of a buiIding are 50 m Iong, 40m wide and 70m high. A model of the same building is made with a scale factor of 1: 500. Find the dimensions of the model.
A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"EC"`
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate: Length of AB, if A'B' = 5.4cm
