Advertisements
Advertisements
प्रश्न
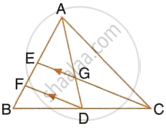
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
- EF = FB,
- AG : GD = 2 : 1
उत्तर
i. In ∆BFD and ∆BEC,
∠BFD = ∠BEC ...(Corresponding angles)
∠FBD = ∠EBC ...(Common)
∆BFD ~ ∆BEC ...(AA Similarity)
∴ `(BF)/(BE) = (BD)/(BC)`
`(BF)/(BE) = 1/2` ...(As D is the mid-point of BC)
BE = 2BF
BF = FE = 2BF
Hence, EF = FB
ii. In ΔAFD, EG || FD.
Using Basic Proportionality theorem,
`(AE)/(EF) = (AG)/(GD)` ...(1)
Now, AE = EB ...(As E is the mid-point of AB)
AE = 2EF ...(Since, EF = FB, by (i))
From (1),
`(AG)/(GD) = 2/1`
Hence, AG : GD = 2 : 1
APPEARS IN
संबंधित प्रश्न
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
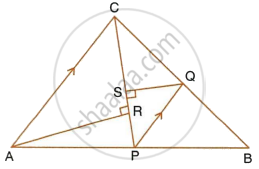
- Calculate the ratio PQ : AC, giving reason for your answer.
- In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`
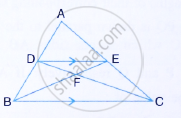
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`
(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.
(3) What is the ratio of the areas of ∆DEF and ∆BFC.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

An aeroplane is 30 m long and its model is 15 cm long. If the total outer surface area of the model is 150 cm2, find the cost of painting the outer surface of the aeroplane at the rate of Rs.120 per sq. m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
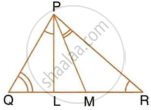
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that:
- ΔPQL ∼ ΔRPM
- QL × RM = PL × PM
- PQ2 = QR × QL
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
Show that:
- ΔADC ∼ ΔBEC
- CA × CE = CB × CD
- ΔABC ~ ΔDEC
- CD × AB = CA × DE
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
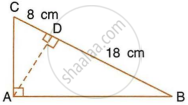
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
