Advertisements
Advertisements
Question
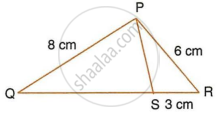
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- Prove ΔPQR ∼ ΔSPR.
- Find the length of QR and PS.
- `"area of ΔPQR"/"area of ΔSPR"`
Solution
i. In ΔPQR and ΔSPR, we have
∠QPR = ∠PSR ...(Given)
∠PRQ = ∠PRS ...(Common)
So, by AA-axiom similarity, we have
ΔPQR ∼ ΔSPR ...(Proved)
ii. Since ΔPQR ∼ ΔSPR ...(Proved)
`=> (PQ)/(SP) = (QR)/(PR) = (PR)/(SR)`
Consider `(QR)/(PR) = (PR)/(SR)` ...(From 1)
`=> (QR)/6 = 6/3`
`=> QR = (6 xx 6)/3 = 12 cm`
Also, `(PQ)/(SP) = (PR)/(SR)`
`=> 8/(SP) = 6/3`
`=>8/(SP) = 2`
`=> SP = 8/2 = 4 cm`
iii. `"area of ΔPQR"/"area of ΔSPR" = (PQ^2)/(SP^2)`
= `8^2/4^2`
= `64/16`
= `4/1`
`"area of ΔPQR"/"area of ΔSPR" = 4 : 1`
APPEARS IN
RELATED QUESTIONS
Given: ABCD is a rhombus, DPR and CBR are straight lines.
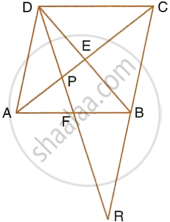
Prove that: DP × CR = DC × PR.
In ∆ABC, right – angled at C, CD ⊥ AB.
Prove:
`"CD"^2 = "AD"xx "DB"`
In the right-angled triangle QPR, PM is an altitude.
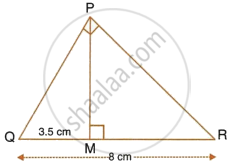
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
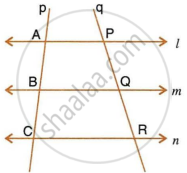
Prove that : `(AB)/(BC) = (PQ)/(QR)`
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.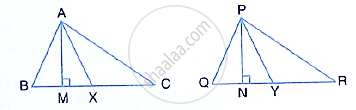 Prove that : `(AM)/(PN)=(AX)/(PY)`
Prove that : `(AM)/(PN)=(AX)/(PY)`
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ΔDEF such that the longest side of ΔDEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ΔDEF.
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In triangle ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA.
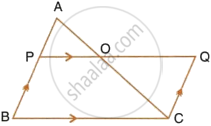
Find:
- area ΔAPO : area ΔABC.
- area ΔAPO : area ΔCQO.
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
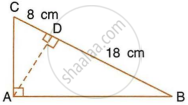
- Prove that : ΔADB ∼ ΔCDA.
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ΔADB is to area of ΔCDA.
