Advertisements
Advertisements
प्रश्न
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : `("AB")/("PQ") = ("AD")/("PM")`.
उत्तर
Given, ΔABC ∼ ΔPQR; AD and PM are the medians of ΔABC and ΔPQR respectively.
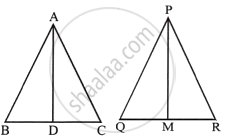
To prove: `("AB")/("PQ") = ("AD")/("PM")`
Proof: Since, ΔABC ∼ ΔPQR
∴ ∠B = ∠Q and
`("AB")/("PQ") = ("BC")/("QR") = (2"BD")/(2"QM") = ("BD")/("QM")` ...(∵ D and M are mid-points of BC and QR)
Now in ΔABD and ΔPQM
`("AB")/("PQ") = ("BD")/("QM")` ...(Proved)
∠B = ∠Q ...(Given)
∴ ΔABD ∼ ΔPQM ...(SAS axiom of similarity)
∴ `("AB")/("PQ") = ("AD")/("PM")` ...(Corresponding sides of Δ's are proportional)
APPEARS IN
संबंधित प्रश्न
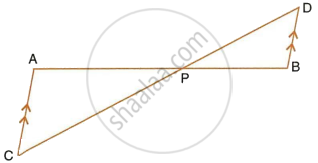
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
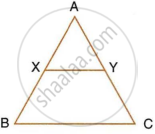
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
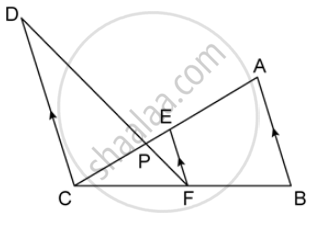
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the given figure ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ∼ Δ AMP.
(ii) Find AB and BC.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
