Advertisements
Advertisements
प्रश्न
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
उत्तर
In ΔABC and ΔDEF, AC = 19 cm, DF = 8 cm.
Since, `"area (Δ ABC)"/"area (Δ DEF)" = "AC"^2/"DF"^2 = (19)^2/(8)^2 = (361)/(64)`
Hence, the required ratio is 361: 64.
APPEARS IN
संबंधित प्रश्न
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

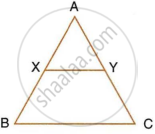
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
Find : XY
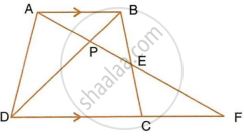
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
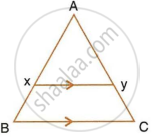
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
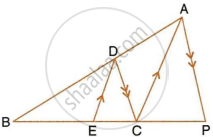
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
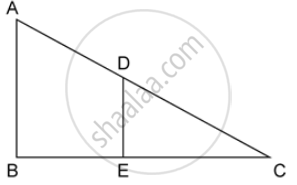
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
