Advertisements
Advertisements
Question
In the given figure ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ∼ Δ AMP.
(ii) Find AB and BC.
Solution
In ΔABC and ΔAMP
i)
∠ABC = ∠AMP ...(90° each)
∠BAC = ∠PAM ...(common angles)
∴ ΔABC ∼ ΔAMP ...(by AA similarity)
Hence proved.
(ii) ΔABC ∼ ΔAMP
⇒ `"AB"/"AM" = "BC"/"PM" = "AC"/"AP"`
⇒ `"BC"/"PM" = "AC"/"AP"`
⇒ `"BC"/(12) = (10)/(15)`
⇒ BC = `(10)/(15) xx 12`
BC = 8
Now, AB2 = AC2 - BC2
= 102 - 82
= 100 - 64 = 36
AB = 6 cm.
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
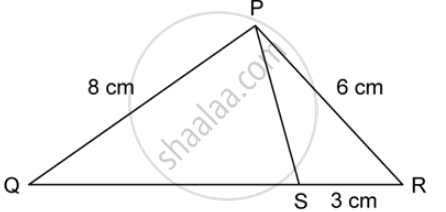
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
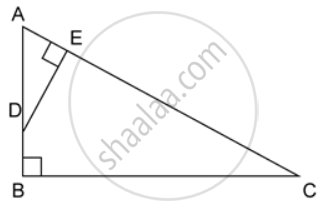
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
