Advertisements
Advertisements
प्रश्न
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
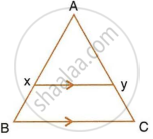
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
उत्तर
i. Given that XY || BC
So, ΔAXY ∼ ΔABC
`=> (AY)/(YC) = 9/4.5`
`=> (AY)/(YC) = 2/1`
`=> (AY)/(YC) = 2`
ii. Given that XY || BC
So, ΔAXY ∼ ΔABC
`=> (AX)/(AB) = (AY)/(AC)`
`=> (AY)/(AC) = 1/(2 + 1)`
`=> (YC)/(AC) = 1/3`
iii. In ΔAXY and ΔABC,
∠XAY = ∠BAC ...(Common angle)
∠AXY = ∠ABC ...(Corresponding angles for parallel lines, XY || BC)
∠AYX = ∠ACB ...(Corresponding angles for parallel lines, XY || BC)
Thus, ΔAXY ∼ ΔABC
Hence, `(AX)/(AB) = (XY)/(BC)` ...(Using similar triangle property)
`(AX)/(AX + XB) = (XY)/18`
`9/(9 + 4.5) = (XY)/18`
`XY = (18 xx 9)/(13.5)`
XY = 12 cm
APPEARS IN
संबंधित प्रश्न
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
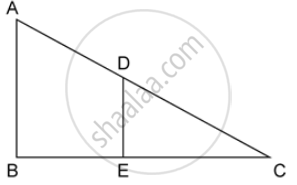
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and DE = 5.1 cm, find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
