Advertisements
Advertisements
प्रश्न
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
उत्तर
In the triplet (10, 24, 27),
102 = 100, 242 = 576, 272 = 729 and 100 + 576 = 676 ≠ 729
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (10, 24, 27) is not a pythagorean triplet.
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
Find the unknown side in the following triangles
Find the length of the support cable required to support the tower with the floor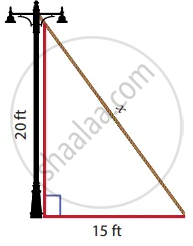
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
