Advertisements
Advertisements
Question
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
Solution
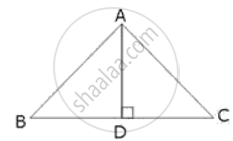
In equilateral triangle AD ⊥ BC.
⇒ BD = DC = `"BC"/(2)` ...(In equilateral triangle altitude bisects the opposite side)
In right triangle ABD,
AB2 = AD2 + BD2
= `"AD"^2 + ("BC"/2)^2`
= `(4"AD"^2 + "BC"^2)/(4)`
= `(4"AD"^2 + "BC"^2)/(4)` ...(Since AB = BC)
⇒ 4AB2 = 4AD2 + AB2
⇒ 3AB2 = 4AD2
Hence proved..
APPEARS IN
RELATED QUESTIONS
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In the figure below, find the value of 'x'.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Find the unknown side in the following triangles
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
The longest side of a right angled triangle is called its ______.
Two rectangles are congruent, if they have same ______ and ______.
