Advertisements
Advertisements
Question
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
Solution
Hypotenuse = p cm
One side = q cm
Let the length of the third side be x cm.
Using Pythagoras theorem,
x2 = p2 - q2 = (p + q)(p - q)
= (p ++ q) x 1 ...[∵ p - q = 1, given]
= p + q
∴ x = `sqrt("p" + "q")`
Thus, the length of the third side of the triangle is `sqrt("p" + "q")"cm"`.
APPEARS IN
RELATED QUESTIONS
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.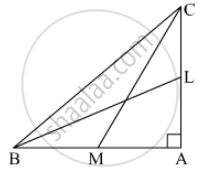
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
