Advertisements
Advertisements
प्रश्न
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

उत्तर
Let ∠CAB = x
In ΔCBA,
∠CBA = 180° - 90° - x
∠CBA = 90° - x
Similarly, in ΔCAD
∠CAD = 90° - ∠CBA
= 90° - x
∠CDA = 180° - 90° - (90° - x)
∠CDA = x
In ΔCBA and ΔCAD, we have
∠CBA = ∠CAD
∠CAB = ∠CDA
∠ACB = ∠DCA (Each equals to 90°)
∴ ΔCBA ~ ΔCAD [By AAA similarity criterion]
`⇒ (AC)/(DC) = (BC)/(AC)`
⇒ AC2 = DC × BC
APPEARS IN
संबंधित प्रश्न
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Find the side of the square whose diagonal is `16sqrt(2)` cm.
In the figure below, find the value of 'x'.
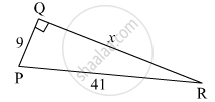
Find the Pythagorean triplet from among the following set of numbers.
9, 40, 41
Find the unknown side in the following triangles
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
