Advertisements
Advertisements
प्रश्न
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
उत्तर
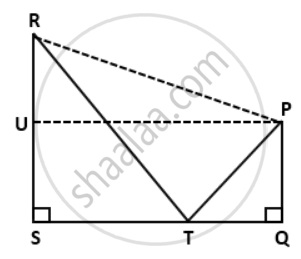
PQ = `"RS"/(3)` = 8cm
⇒ PQ = 8cm and RS = 3 x 8 = 24cm
3ST = 4QT = 48cm
⇒ ST = `(48)/(3) = 16"cm" and "QT" = (48)/(4)` = 12cm
In ΔPTQ,
PT2 = PQ2 + QT2
= 82 + 122
= 64 + 144
= 208
In ΔRTS,
RT2 = RS2 + ST2
= 242 + 162
= 576 + 256
= 832
Now, PT2 + RT2
= 208 + 832
= 1040 .....(i)
Draw PU ⊥ RS and Join PR.
PU = SQ
= ST + TQ
= 16 + 12
= 28cm
RU = RS - US
= RS - PQ
= 24 - 8
= 16cm
In ΔRUP,
PR2 = RU2 + PU2
= 162 + 282
= 256 + 784
= 1040 ....(ii)
From (i) and (ii), we get
PT2 + RT2 = PR2
Thus, ∠RTP = 90°.
APPEARS IN
संबंधित प्रश्न
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Find the unknown side in the following triangles
Find the distance between the helicopter and the ship
