Advertisements
Advertisements
Question
In Fig below we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.

Solution
We have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm
In ΔECD and ΔEAB
∠CED = ∠AEB [common]
∠ECD = ∠EAB [corresponding angles]
Then, ΔECD ~ ΔEAB ….(i) [By AA similarity]
`therefore"EC"/"EA"="CD"/"AB"` [Corresponding parts of similar Δ are proportional]
`rArr"EC"/"EA"=x/6` .........(ii)
In ΔACD and ΔAEF
∠CAD = ∠EAF [common]
∠ACD = ∠AEF [corresponding angles]
Then, ΔACD ~ ΔAEF [By AA similarity]
`therefore"AC"/"AE"="CD"/"EF"`
`rArr"AC"/"AE"=x/10` ..........(iii)
Add equations (iii) & (ii)
`therefore"EC"/"EA"+"AC"/"AE"=x/6+x/10`
`rArr"AE"/"AE"=(5x+3x)/30`
`rArr1=(8x)/30`
`rArrx=30/8=3.75` cm
From (i) "DC"/"AB"="ED"/"BE"
`rArr3.75/6=y/(y+4)`
⇒ 6y = 3.75y + 15
⇒ 2.25y = 15
`rArry=15/2.25=6.67` cm
APPEARS IN
RELATED QUESTIONS
In the following figure, ABC and AMP are two right triangles, right-angled at B and M respectively, prove that:

- ΔABC ~ ΔAMP
- `("CA")/("PA") = ("BC")/("MP")`
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
In the given figure, value of x(in cm) is

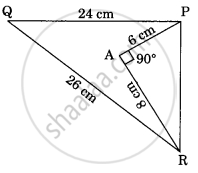
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
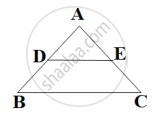
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

