Advertisements
Advertisements
प्रश्न
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
उत्तर
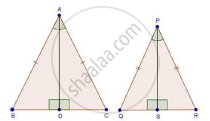
Given: AB = AC, PQ = PQ and ∠A = ∠P
And, AD and PS are altitudes
And, `("Area"(triangleABC))/("Area"(trianglePQR))=36/25` .........(i)
To find `"AD"/"PS"`
Proof: Since, AB = AC and PQ = PR
Then, `"AB"/"AC"=1` and `"PQ"/"PR"=1`
`therefore"AB"/"AC"="PQ"/"PR"`
`rArr"AB"/"PQ"="AC"/"PR"` ........(ii)
In ΔABC and ΔPQR
∠A = ∠P [Given]
`"AB"/"PQ"="AC"/"PR"` [From (2)]
Then, ΔABC ~ ΔPQR [By SAS similarity]
`therefore("Area"(triangleABC))/("Area"(trianglePQR))="AB"^2/"PQ"^2` .....(iii) [By area of similar triangle theorem]
Compare equation (i) and (iii)
`"AB"^2/"PQ"^2=36/25`
`"AB"/"PQ"=6/5` ..........(iv)
In ΔABD and ΔPQS
∠B = ∠Q [ΔABC ~ ΔPQR]
∠ADB = ∠PSQ [Each 90°]
Then, ΔABD ~ ΔPQS [By AA similarity]
`therefore"AB"/"PQ"="AD"/"PS"`
`rArr6/5="AD"/"PS"` [From (iv)]
APPEARS IN
संबंधित प्रश्न
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half the area of the similar Triangle ACF described on the diagonal AC as base
Two isosceles triangles have equal vertical angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights
In ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ΔAPQ and trapezium BPQC.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find the length of QR.
If D is a point on the side AB of ΔABC such that AD : DB = 3.2 and E is a Point on BC such that DE || AC. Find the ratio of areas of ΔABC and ΔBDE.
∆LMN ~ ∆PQR, 9 × A (∆PQR ) = 16 × A (∆LMN). If QR = 20 then Find MN.
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
If ΔABC ~ ΔPQR, AB : PQ = 4 : 5 and A(ΔPQR) = 125 cm2, then find A(ΔABC).
If the perimeter of two similar triangles is in the ratio 2 : 3, what is the ratio of their sides?
If ΔPQR ∼ ΔABC; PQ = 6 cm, AB = 8 cm and the perimeter of ΔABC is 36 cm, then the perimeter of ΔPQR is ______.
