Advertisements
Advertisements
Question
From a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Use π = 3.14)
Solution
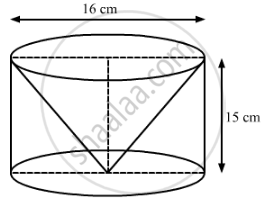
We have,
Height of the cylinder = Height of the cone = h = 15 cm and
Radius of thecylinder = Radius of the cone `= r = 16/2 = 8 "cm" `
Also, the slant height of the cone, `l =sqrt("h"^2 + "r"^2)`
`=sqrt(15^2 + 8^2)`
`=sqrt(225+64)`
`=sqrt(289)`
= 17 cm,
Now,
Then total surface area of the remaining solid = CSA of the cone + CSA of the cone + Area of the base
=πrl+ 2πrh + πr2
= πr (l + 2h + r)
= 3.14 × 8× (17 + 2 × 15 + 8)
= 3.1× 8 × 55
= 1381.6 cm2
So, the total surface area of the remaining solid is 1381.6 cm2.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
RELATED QUESTIONS
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
Assertion (A)
If the volumes of two spheres are in the ratio 27 : 8, then their surface areas are in the ratio 3 : 2.
Reason (R)
Volume of a sphere `=4/3pi"R"^3`
Surface area of a sphere = 4πR2
Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
If the side of a cube is 5 cm, then find its volume.
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
A surahi is the combination of ______.
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
______ surface area of room = area of 4 walls.
