Advertisements
Advertisements
प्रश्न
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
उत्तर
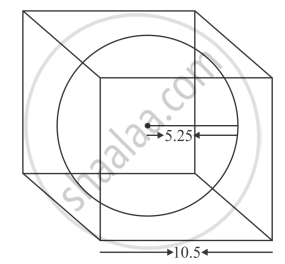
The side of cube a = 10.5 cm.
Since, a largest sphere is curved out of that cube
i.e., radius of sphere,
`r = a/2`
`r= (10.5)/2 cm`
`r = 5.25 cm`
The volume of sphere
`= 4/3 pi (5.25)^3`
`=4/3 xx 22/7 xx 5.25 xx 5.25 xx 5.25`
` = 22 xx 0.75 xx 1.75 xx 21`
` = 606.375 cm^3`
APPEARS IN
संबंधित प्रश्न
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond ?
A solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm.Find the number of cones so formed.
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
A hemispherical bowl of internal radius 9 cm is full of liquid . The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm . How many bottles are needed to empty the bowl ?
If the radii of the circular ends of a bucket of height 40 cm are of lengths 35 cm and 14 cm, then the volume of the bucket in cubic centimeters, is
A spherical ball of diameter 21 cm is melted and recast into cubes, each of side 1 cm. Find the number of cubes so formed.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is ______.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3 . the radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height.
