Advertisements
Advertisements
प्रश्न
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is ______.
पर्याय
2.1
4.2
8.4
1.05
उत्तर
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is 2.1.
Explanation:
Since, the diameter of the base of the largest cone that can be cut out from the cube = Edge of the cube = 4.2 cm
So, the radius of the base of the largest cone
= `4.2/2` = 2.1 cm
APPEARS IN
संबंधित प्रश्न
The `3/4` th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3·5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
Water flows through a cylindrical pipe , whose inner radius is 1 cm , at the rate of 80 cm /sec in an empty cylindrical tank , the radius of whose base is 40 cm . What is the rise of water level in tank in half an hour ?
A wall 24 m , 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm \[\times\] 16 cm \[\times\] 10 cm . If the mortar occupies \[\frac{1}{10}th\] of the volume of the wall, then find the number of bricks used in constructing the wall.
Water flows at the rate of 10 metre per minute from a cylindrical pipe 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter at the base is 40 cm and depth 24 cm?
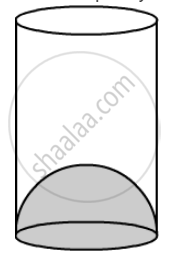
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
The dimensions of a metallic cuboid are 100cm× 80 cm× 64cm. It is melted and recast into a cube. Find the surface area of the cube.
The radii of the top and bottom of a bucket of slant height 45cm are 28cm and 7 cm respectively. The curved surface area of the bucket is ______.
______ surface area of room = area of 4 walls.
