Advertisements
Advertisements
प्रश्न
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs Rs. 100 per sq. m, find the amount, the associations will have to pay. What values are shown by these associations? [Use π=22/7]
उत्तर
Diameter of the tent = 4.2 m
Radius of the tent, r = 2.1 m
Height of the cylindrical part of tent, hcylinder = 4 m
Height of the conical part, hcone = 2.8 m
Slant height of the conical part, l
`=sqrt(h_(`
`=sqrt((2.8)^2+(2.1)^2)`
`=sqrt(12.5)=3.5m`
Curved surface area of the cylinder = 2𝜋r hcylinder
= 2 ×(22/7)× 2.1 × 4
= 22 × 0.3 × 8 = 52.8 m2
Curved surface area of the conical tent = 𝜋rl =(22/7)× 2.1 × 3.5 = 23.1 m2
Total area of cloth required for building one tent
= Curved surface area of the cylinder + Curved surface area of the conical tent
= 52.8 + 23.1
= 75.9 m2
Cost of building one tent = 75.9 × 100 = Rs. 7590
Total cost of 100 tents = 7590 × 100 = Rs. 7,59,000
Cost to be borne by the associations =759000/2= Rs. 3,79,500
It shows the helping nature, unity and cooperativeness of the associations.
APPEARS IN
संबंधित प्रश्न
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
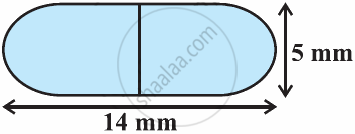
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
A bucket has top and bottom diameter of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs. 1.20 per dm2 . (Use π = 3.14)
A metallic cylinder has radius 3 cm and height 5 cm. To reduce its weight, a conical hole is drilled in the cylinder. The conical hole has a radius of `3/2` cm and its depth is `8/9 `cm. Calculate the ratio of the volume of metal left in the cylinder to the volume of metal taken out in conical shape.
A solid cuboid of iron with dimensions 53 cm ⨯ 40 cm ⨯ 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe.
Water is flowing through a cylindrical pipe of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m per second. Determine the rise in level of water in the tank in half an hour.
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is ______.

A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m2 of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m2.
