Advertisements
Advertisements
प्रश्न
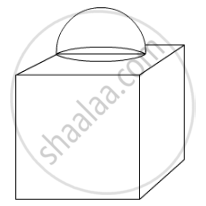
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
उत्तर
First Solid |
Second Solid |
i. Surface Area for first new solid (S1):
6 × 7 × 7 + 2π × 3.52 – π × 3.52
= 294 + 77 – 38.5
= 332.5 cm2
Surface Area for second new solid (S2):
6 × 7 × 7 + 2π × 3.52 – π × 3.52
= 294 + 77 – 38.5
= 332.5 cm2
So S1: S2 = 1 : 1
ii. Volume for first new solid (V1) = `7 xx 7 xx 7 - 2/3 π xx 3.5^3`
= `343 - 539/6`
= `1519/6` cm3
Volume for second new solid (V2) = `7 xx 7 xx 7 + 2/3 π xx 3.5^3`
= `343 + 539/6`
= `2597/6` cm3
APPEARS IN
संबंधित प्रश्न
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of Rs. 5 per 100 sq. cm. [Use π = 3.14]
The largest possible sphere is carved out of a wooden solid cube of side 7 em. Find the volume of the wood left. (Use\[\pi = \frac{22}{7}\]).
In Fig. 5, is a decorative block, made up two solids – a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has diameter of 3.5 cm. Find the total surface area of the bock `(Use pi=22/7)`
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. `("use " pi=22/7)`
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm. and 6 cm, respectively. Find the total surface area of the solid. (Use π =`22/7`)
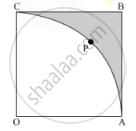
In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. `[\text\ User=22/7]`
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
