Advertisements
Advertisements
Question
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution
Let AB be the platform of the fire brigade van and AD be the ladder.
Suppose the maximum height from the ground upto which the ladder can reach be h m.
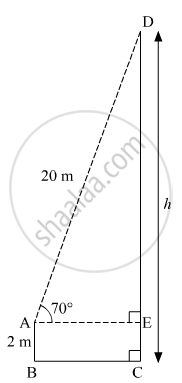
Here, AB = 2 m, AD = 20 m, ∠DAE = 70º and AE ⊥ CD.
DE = CD − CE = (h − 2) m (CE = AB)
In right ∆AED,
\[\sin70^\circ = \frac{DE}{AD}\]
\[ \Rightarrow 0 . 94 = \frac{h - 2}{20}\]
\[ \Rightarrow h - 2 = 20 \times 0 . 94 = 18 . 8\]
\[ \Rightarrow h = 18 . 8 + 2 = 20 . 8 m\]
Thus, the maximum height from the ground upto which the ladder can reach is 20.8 m.
APPEARS IN
RELATED QUESTIONS
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.

