Advertisements
Advertisements
प्रश्न
A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that `p/q = (cos β - cos α)/(sin α - sin β)`
उत्तर
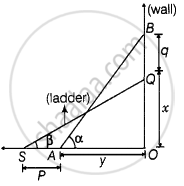
Let OQ = x and OA = y
Given that, BQ = q, SA = P and AB = SQ = Length of ladder
Also, ∠BAO = α and ∠QSO = β
Now, In ΔBAO,
cos α = `"OA"/"AB"`
⇒ cos α = `y/"AB"`
⇒ y = AB cos α = OA ...(i)
And sin α = `"OB"/"AB"`
⇒ OB = BA sin α ...(ii)
Now, In ΔQSO
cos β = `"OS"/"SQ"`
⇒ OS = SQ cos β = AB cos β ...[∵ AB = SQ] ...(iii)
And sin β = `"OQ"/"SQ"`
⇒ OQ = SQ sin β = AB sin β ...[∵ AB = SQ] ...(iv)
Now, SA = OS – AO
P = AB cos β – AB cos α
⇒ P = AB(cos β – cos α) ...(v)
And BQ = BO – QO
⇒ q = BA sin α – AB sin β
⇒ q = AB(sin α – sin β) ...(vi)
Equation (v) divided by Equation (vii), we get
`"p"/"q" = ("AB"(cos β - cos α))/("AB"(sin α - sin β)) = (cos β - cos α)/(sin α - sin β)`
⇒ `"p"/"q" = (cos β - cos α)/(sin α - sin β)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`cos theta = 12/2`
If tan θ = `a/b` prove that `(a sin theta - b cos theta)/(a sin theta + b cos theta) = (a^2 - b^2)/(a^2 + b^2)`
if `tan theta = 12/13` Find `(2 sin theta cos theta)/(cos^2 theta - sin^2 theta)`
If `sin theta = a/b` find sec θ + tan θ in terms of a and b.
If Cosec A = 2 find `1/(tan A) + (sin A)/(1 + cos A)`
Evaluate the following
sin2 30° + sin2 45° + sin2 60° + sin2 90°
The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is ______.
If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to ______.
Given that sinα = `1/2` and cosβ = `1/2`, then the value of (α + β) is ______.
Prove that: cot θ + tan θ = cosec θ·sec θ
Proof: L.H.S. = cot θ + tan θ
= `square/square + square/square` ......`[∵ cot θ = square/square, tan θ = square/square]`
= `(square + square)/(square xx square)` .....`[∵ square + square = 1]`
= `1/(square xx square)`
= `1/square xx 1/square`
= cosec θ·sec θ ......`[∵ "cosec" θ = 1/square, sec θ = 1/square]`
= R.H.S.
∴ L.H.S. = R.H.S.
∴ cot θ + tan θ = cosec·sec θ
