Advertisements
Advertisements
рдкреНрд░рд╢реНрди
if `tan theta = 12/13` Find `(2 sin theta cos theta)/(cos^2 theta - sin^2 theta)`
рдЙрддреНрддрд░
Let x be, the hypotenuse
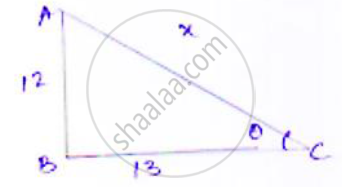
By Pythagoras we get
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2
ЁЭСе2 = 144 + 169
`x = sqrt313`
`sin theta = (AB)/(AC) = 12/sqrt313`
`cos theta = (BC)/(AC) = 13/sqrt313`
Substitute, Sin ЁЭЬГ, cos ЁЭЬГ in equation we get
`(2 sin theta cos theta)/(cos^2 theta - sin^2 theta) => (2 xx 12/sqrt313 xx 13/sqrt313)/(169/313 - 144/313)`
`= (312/313)/(25/313) = 312/25`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
Given sec θ = `13/12`, calculate all other trigonometric ratios.
Evaluate the Following
`(sin 30^@ - sin 90^2 + 2 cos 0^@)/(tan 30^@ tan 60^@)`
Evaluate the Following:
`tan 45^@/(cosec 30^@) + sec 60^@/cot 45^@ - (5 sin 90^@)/(2 cos 0^@)`
Find the value of x in the following :
`sqrt3 sin x = cos x`
Find the value of x in the following :
`sqrt3 tan 2x = cos 60^@ + sin45^@ cos 45^@`
Find the value of x in the following :
cos 2x = cos 60° cos 30° + sin 60° sin 30°
If cos A = `4/5`, then the value of tan A is ______.
Prove that `tan θ/(1 - cot θ) + cot θ/(1 - tanθ)` = 1 + sec θ cosec θ
If cosec θ = `("p" + "q")/("p" - "q")` (p ≠ q ≠ 0), then `|cot(π/4 + θ/2)|` is equal to ______.
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
