Advertisements
Advertisements
प्रश्न
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
उत्तर
We have
`cos theta == 5/13`
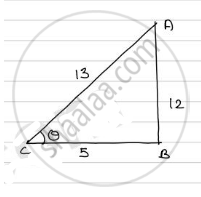
In Δ ABC
`AC^2 = AB^2 + BC^2`
`=>(13)^2 = (AB)^2 + (5)^2`
`=> 169 = (AB)^2 + 25`
`=> (AB)^2 = 169 - 25`
=> AB = 12
`:. sin theta = 12/13 and tan theta = 12/5`
Now
`(sin^2 theta - cos^2 theta) xx 1/tan^2 theta = ((12/13)^2 - (5/13)^2)/(2 xx 12/13 xx 5/13) xx 1/(12/5)^2`
`= ((144 - 25)/169)/(120/169) xx 25/144`
`= 119/120 xx 25/144`
`= (119 xx 5)/(24 xx 144) = 595/3456`
APPEARS IN
संबंधित प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If cos θ=0.6 show that (5sin θ -3tan θ) = 0
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos C
From the given figure, find the values of sin B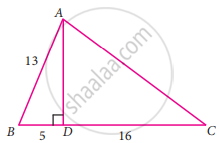
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
