Advertisements
Advertisements
Question
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
Solution
We have
`cos theta == 5/13`
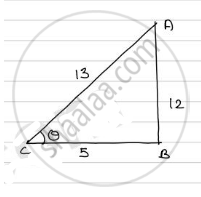
In Δ ABC
`AC^2 = AB^2 + BC^2`
`=>(13)^2 = (AB)^2 + (5)^2`
`=> 169 = (AB)^2 + 25`
`=> (AB)^2 = 169 - 25`
=> AB = 12
`:. sin theta = 12/13 and tan theta = 12/5`
Now
`(sin^2 theta - cos^2 theta) xx 1/tan^2 theta = ((12/13)^2 - (5/13)^2)/(2 xx 12/13 xx 5/13) xx 1/(12/5)^2`
`= ((144 - 25)/169)/(120/169) xx 25/144`
`= 119/120 xx 25/144`
`= (119 xx 5)/(24 xx 144) = 595/3456`
APPEARS IN
RELATED QUESTIONS
Given 15 cot A = 8. Find sin A and sec A.
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If cos θ = `7/25` find the value of all T-ratios of θ .
If cot θ = 2 find all the values of all T-ratios of θ .
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
`(cos 28°)/(sin 62°)` = ?
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
If tan = 0.75, find the other trigonometric ratios for A.
If sin A = `(7)/(25)`, find the value of : `(2"tanA")/"cot A - sin A"`
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
