Advertisements
Advertisements
Question
If cot θ = 2 find all the values of all T-ratios of θ .
Solution
Let us first draw a right ΔABC, right angled at B and ∠𝐶 = 𝜃
Now, we know that cot θ = `"𝐵𝑎𝑠𝑒"/" 𝑃𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟" = (BC)/(AB) = 2`
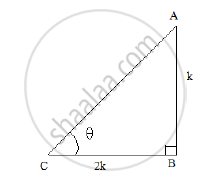
So, if BC = 2k, then AB = k, is a positive number.
Now, using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2 = (2K)^2 + (K)^2`
`⟹ AC^2 = 4K^2 + K^2 = 5K^2`
`⟹ AC= sqrt(5k)`
Now, finding the other T-ratios using their definitions, we get:
Sin θ = `(AB)/(AC) = 5/(sqrt(5k)) = 1/(sqrt (2)`
∴ Cos θ = `1/ (cot θ ) = 1/2 , cosec θ = 1/(sin θ ) = sqrt(5) and secθ = 1/ (cos θ) = sqrt(5)/2`
APPEARS IN
RELATED QUESTIONS
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
If 8 tan A = 15, find sin A – cos A.
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
Prove that
cosec (65 °+ θ) sec (25° − θ) − tan (55° − θ) + cot (35° + θ) = 0
In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm.
find :
- tan ∠DBC
- sin ∠DBA

In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P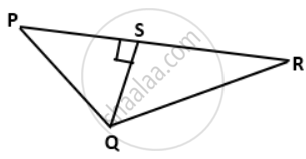
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of sin x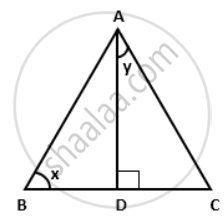
From the given figure, find the values of sec B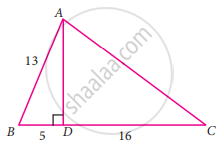
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
