Advertisements
Advertisements
Question
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of sin x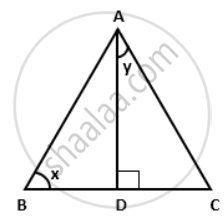
Solution
Since AD is median on BC, we have
BD = DC = `(1)/(2) xx "BC" = (1)/(2) xx 12` = 6cm
ΔADB is a right-angled triangle.
∴ AB2
= AD2 + BD2
= 82 + 62
= 64 + 36
= 100
⇒ AB = 10cm
ΔADC is a right-angled triangle.
∴ AC2
= AD2 + DC2
= 82 + 62
= 64 + 36
= 100
⇒ AC = 10cm
sin x
= `"AD"/"AB"`
= `(8)/(10)`
= `(4)/(5)`.
APPEARS IN
RELATED QUESTIONS
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
If cos θ = `7/25` find the value of all T-ratios of θ .
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
From the given figure, find all the trigonometric ratios of angle B
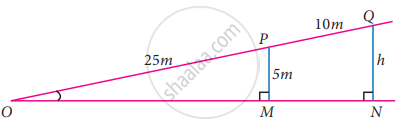
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)