Advertisements
Advertisements
Question
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
Solution
tanB = `(8)/(15)`
tanB = `"Perpendicular"/"Base" = (8)/(15)`
By Pythagoras theorem, we have
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
(Hypotenuse) = `sqrt(("Perpendicular")^2 + ("Base")^2`
= `sqrt((8)^2 + (15)^2`
= `sqrt(64 + 225)`
= `sqrt(289)`
= 17
cot B = `(1)/"tan B" = (15)/(8)`
sin B = `"Perpendicular"/"Hypotenuse" = (8)/(17)`
cos B = `"Base"/"Hypotenuse" = (15)/(17)`
sec B = `(1)/"cos B" = (17)/(15)`
cosec B = `(1)/"sin B" = (17)/(8)`.
APPEARS IN
RELATED QUESTIONS
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ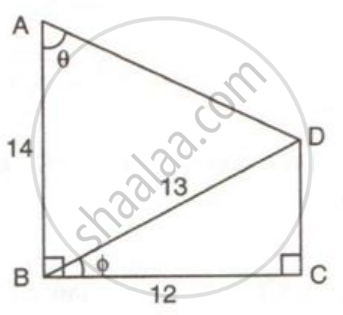
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos C
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
