Advertisements
Advertisements
Question
Find acute angles A & B, if sin (A + 2B) =
Solution
Sin (A + 2B) = Sin 60°
Cos (A + 4B) = cos 90°
A + 2B = 60° …(i)
A + 4B = 90° …(ii)
Subtracting (ii) from (i)
A + 4B = 90°
A + 4B = 90°
4B = 4(15°) = 4B = 60°
∴ A + 60° = 90° ∴ A = 30°
APPEARS IN
RELATED QUESTIONS
In Fig below, Find tan P and cot R. Is tan P = cot R?

If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
If sin θ =
Evaluate:
cos600 cos300− sin600 sin300
If sin (A – B) =
tan 30° × tan ______° = 1
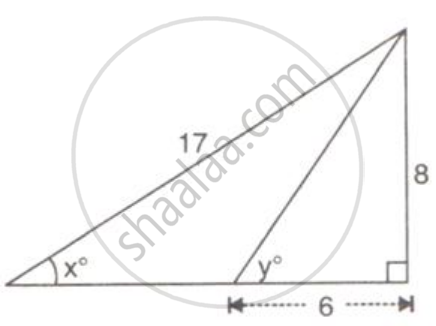
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
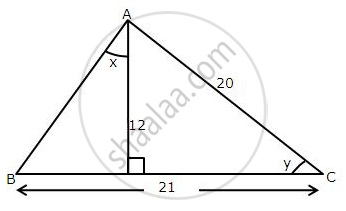
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) 
Use the information given in the following figure to evaluate:
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P