Advertisements
Advertisements
प्रश्न
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
उत्तर
Sin (A + 2B) = Sin 60°
Cos (A + 4B) = cos 90°
A + 2B = 60° …(i)
A + 4B = 90° …(ii)
Subtracting (ii) from (i)
A + 4B = 90°
`(−A – 2B = −60)/(2B = 30°)` ∴ B = 15°
A + 4B = 90°
4B = 4(15°) = 4B = 60°
∴ A + 60° = 90° ∴ A = 30°
APPEARS IN
संबंधित प्रश्न
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
In a ΔABC , ∠B = 90° , AB= 24 cm and BC = 7 cm find (i) sin A (ii) cos A (iii) sin C (iv) cos C
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
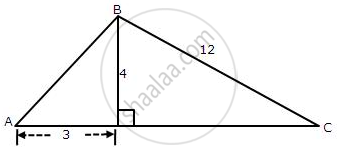
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
If cos A = `(1)/(2)` and sin B = `(1)/(sqrt2)`, find the value of: `(tan"A" – tan"B")/(1+tan"A" tan"B")`.
Are angles A and B from the same triangle? Explain.
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
