Advertisements
Advertisements
प्रश्न
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
उत्तर
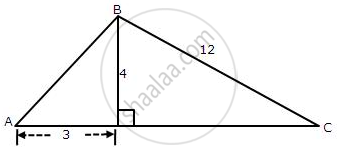
Consider the diagram as
Given angle ADB = 90° and BDC = 90°
⇒ AB2 = AD2 + BD2 ...( AB is hypotenuse in ΔABD )
⇒ AB2 = 32 + 42
∴ AB2 = 9 + 16 = 25 and AB = 5
⇒ BC2 = BD2 + DC2 ...( BC is hypotenuse in ΔBDC )
⇒ DC2 = 122 - 42
∴ DC2 = 144 - 16 = 128 aand DC = 8`sqrt2`
(i) cos A = `"base"/"hypotenuse" = "AD"/"AB" =3/5`
(ii) cosec A = `"hypotenuse"/"perpendicular" = "AB"/"BD" =5/4`
(iii) tan A = `"perpendicular"/"base" = "BD"/"AD" =4/3`
sec A = `"hypotenuse"/"base" = "AB"/"AD" =5/3`
tan2 A - sec2 A = `(4/3)^2 - (5/3)^2`
= `16/9 - 25/9`
= `( – 9)/(9)`
= – 1
(iv) sin C = `"perpendicular"/"hypotenuse" = "BD"/"BC" = 4/12 = 1/3`
(v) sec C = `"hypotenuse"/"base" = "BC"/"DC" = 12/(8sqrt2) = 3/(2sqrt2) = (3sqrt2)/4`
(vi) cot C = `"base"/"perpendicular" = "DC"/"BD" = (8sqrt2)/4 = 2sqrt2`
sin C = `"perpendicular"/"hypotenuse" = "BD"/"BC" = 4/12 = 1/3`
cot2 C – ` 1/sin^2C = (2sqrt2)^2 - 1/(1/3)^2`
= 8 - 9
= – 1
APPEARS IN
संबंधित प्रश्न
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
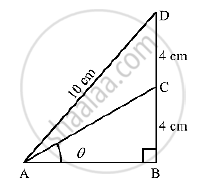
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
From the given figure, find all the trigonometric ratios of angle B
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
